Projectile Motion

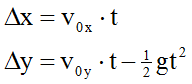
The formulas for projectile motion are identical to those of kinematics, except that the x- and y-components of displacement and velocity are treated separately. In most cases, the horizontal acceleration is zero and the vertical acceleration is directed straight down with a value of g=9.8 m/s².

Sample problem: The cliff divers of Acapulco push off horizontally from rock platforms about 35 m above the water, but they must clear rocky outcrops at water level that extend out into the water 5 m from the base of the cliff directly under their launch point. What minimum push-off speed is required to achieve this? How long are they in the air?

Solution: This is a straight-forward projectile motion problem with a horizontally directed launch.

Sample problem: A mountain climber encounters a crevasse in an ice field. The opposite side of the crevasse is 2.75 m lower and is separated horizontally by a distance of 12 m. To cross the crevasse, the climber gets a running start and takes off horizontally. Will the climber make it safely cross? Would he make it with a take-off angle of 30º? What angle would require the least take-off speed?
Solution:

To figure out the minimum velocity, we can solve for the velocity as a function of angle and look at the graph. This Excel sheet demonstrates the procedure.

Sample problem: A basketball player is standing on the floor 10.0 m from the basket, as shown. The height of the basket is 3.05 m, and he shoots the ball at a 40.0^o angle with the horizontal from a height of 2.00 m. At what speed must the player throw the basketball so that the ball goes through the hoop without striking the backboard?
Solution: This is a typical projectile motion problem for which we need to set up two equations (x and y) to solve for two unknowns.

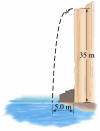
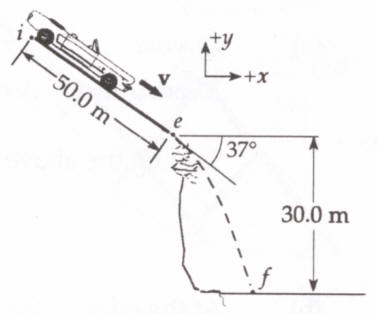
Sample problem: A car is parked on a cliff overlooking the ocean on an incline that makes an angle of 37° below the horizontal. The negligent driver leaves the car in neutral, and the emergency brakes are defective. The car rolls from rest down the incline with a constant acceleration of 4 m/s² for a distance of 50 m to the edge of the cliff. If the cliff is 30 m above the ocean, find the car's position relative to the base of the cliff when the car lands in the ocean.
Solution: This problem combines one-dimensional accelerated motion with projectile motion. It also offers an opportunity to review the quadratic equation.

Range

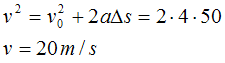
In those cases in which the vertical displacement is zero, the horizontal displacement (also known as range) can be expressed in terms of initial launch speed and angle:

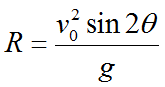
Caution: This formula is only true when the initial and final heights are the same.

When the vertical displacement is zero, complementary launch angles result in the same horizontal range.

Sample problem: A hunter aims his arrow directly at a target (on the same level) 100 m away. If the arrow leaves the bow at a speed of 75 m/s, by how much will it miss the target? What should be the launch angle to hit the target?