Interference of sound waves

• Two initially in-phase speakers interfere destructively when the path difference from them to the listener equals an odd multiple of half-wavelengths.
• Two initially out-of-phase speakers interfere constructively when the path difference from them to the listener equals an odd multiple of half-wavelengths.

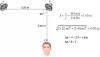
Sample problem: Suppose two in-phase loudspeakers, A and B, are separated by 3.2 m. A listener is stationed at point C, which is 2.4 m in front of speaker B. Both speakers are playing identical 214-Hz tones, and the speed of sound is 343 m/s. Is the sound heard by the listener loud or faint?
Solution: In this example, the path difference is an integer times the wavelength. Since the two speakers are initially in phase, the net effect is constructive interference or loud.

 

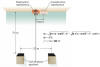
Sample problem: Two out-of-phase speakers are positioned 3.5 m apart, both pointing toward a wall 5 m in front of them. A listener positioned at the wall, midway between the speakers hears virtually nothing (destructive interference). When he moves to one side by 0.84 m, he hears a loud sound (constructive interference). What is the frequency of the sound emitted by the speakers?
Solution:


 

Beats

When two sound waves with similar but not identical frequencies, f₁ and f₂,  interfere with each other, the result is a sound wave with an apparent frequency equal to the average of the two frequencies: f = ½(f₁ + f₂). In addition, this sound wave alternates between loud and faint. This phenomenon is known as beats and the beat frequency is f = ½(f₁ - f₂).

Sample problem: A pop bottle is to be used as a musical instrument in a band. Suppose a 440-Hz tuning fork is used to tune a bottle partly filled with water. Initially a 4-Hz beat frequency is heard. After a small amount of water is added, the beat frequency becomes 5 Hz. What were the initial and final frequencies of the bottle?
Solution: The original frequency is either 436 Hz or 444 Hz. With a little more water, the resonant frequency increases (since the standing-wave wavelength decreases). Since the beat frequency now increases, the original frequency must have been 444 Hz and the new frequency is 445 Hz.

Return to class notes TOC.