Statics
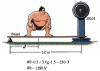
Sample problem: A scale with a capacity of only 250 N can be used to
weigh a heavier person, as shown. The board is 3 m long, has a mass of 3.4 kg,
and is of uniform density. It is free to pivot about the end farthest from the
scale. If the scale reads 230 N with the person standing d = 0.5 m from the
pivot end, what is the weight of the person? Assume that the beam remains nearly
horizontal.
Solution: With a little understanding of statics, we can use a scale with
a relatively low capacity to weigh a very heavy object.
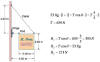
Sample problem: A 53.8-kg uniform square sign, 2.00 m on a side, is hung
from a 3.00 m rod of negligible mass. A cable is attached to the end of the rod
and to a point on the wall 4.00 m above the point where the rod is fixed to the
wall. What is the tension in the cable and the reaction force at the wall?
Solution:
Sample problem: A painter is climbing up a ladder propped up against a
wall. If the mass of the ladder is 11.0 kg, the mass of the painter is 56.5 kg,
and the ladder begins to slip at its base when the painter is 70% of the way up
the length of the ladder, what is the coefficient of static friction between the
ladder and the floor? Assume the wall is frictionless.
Solution: A good choice for the pivot is the contact point of the ladder
with the ground because this choice eliminates the ground force, which is
initially unknown. However, the problem can also be solved with the pivot at the
wall, although the torque equation would then involve an extra term.

Return to class notes TOC.
Page last modified:


