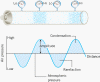
The figure below illustrates a pure-tone sound wave traveling in a tube. Attached to the tube is a series of gauges that indicate the pressure variations along the wave. The graph shows that the air pressure varies sinusoidally along the length of the tube. Although this graph has the appearance of a transverse wave, remember that the sound itself is a longitudinal wave. The graph also shows the pressure amplitude of the wave, which is the magnitude of the maximum change in pressure, measured relative to the undisturbed or atmospheric pressure. The pressure fluctuations in a sound wave are normally very small. For instance, in a typical conversation between two people the pressure amplitude is about 3 × 10-2 Pa, certainly a small amount compared with the atmospheric pressure of 1.01 × 10+5 Pa. The ear is remarkable in being able to detect such small changes.
Sound intensity is often described logarithmically with bels or decibels. I0 corresponds to the lowest intensity detectable by the average human ear.
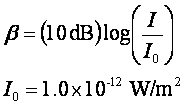
|
I2/I1
|
b2 –
b1
|
|
1
|
10*log(1)= 0
|
|
1.26
|
10*log(1.26)=1
|
|
2
|
10*log(2)=3
|
|
5
|
10*log(5)= 7
|
|
10
|
10*log(10)= 10
|
|
20
|
10*log(20)= 13
|
Sound intensity is defined as power (P) per unit area. Sound intensity of an
isotropic source falls off with an inverse-square dependence.
![]()
We are not equally sensitive to different frequencies, and neither are the animals. In general, the larger animals tend to be more sensitive to lower frequencies, and the smaller animals to higher frequencies. The table below shows the sensitivity ranges for different animals.
|
Animal
|
frequency
low (Hz)
|
frequency
high (Hz)
|
|
Humans
|
20
|
20,000
|
|
Cats
|
100
|
32,000
|
|
Dogs
|
40
|
46,000
|
|
Horses
|
31
|
40,000
|
|
Elephants
|
16
|
12,000
|
|
Cattle
|
16
|
40,000
|
|
Bats
|
1,000
|
150,000
|
|
Grasshoppers and locusts
|
100
|
50,000
|
|
Rodents
|
1,000
|
100,000
|
|
Whales and
dolphins
|
70
|
150,000
|
|
Seals and
sea lions
|
200
|
55,000
|
Sample problem: During a fireworks display, a rocket explodes
high in the air, as shown. Assume that the sound spreads out uniformly in all
directions and that reflections from the ground can be ignored. When the sound
reaches listener 2, who is r2 = 640 m away from the explosion, the
sound has an intensity of I2 = 0.10 W/m2 . What is the
sound intensity detected by listener 1, who is r1 = 160 m away from
the explosion?
Solution:
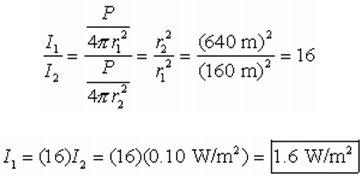
Sample problem: The smallest change in loudness that an average person
can detect is about 1 dB. What percentage increase in intensity does this
represent?
Solution: 1 = 10∙log(x); x = 1.26; or an increase of 26%
Sample problem: Suppose a person talking in a normal voice 2 m away from
you produces a 60-dB sound at your ear. Assuming isotropic propagation of sound,
how much power is delivered by the talking person? What is the intensity level
at a distance of 6 m?
Solution:
![]()
Return to class notes TOC.