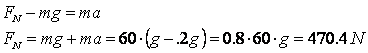
In order to apply Newton's 2nd law, we need to account for all the forces acting on the object and find the resultant. The following is a list of possible forces:
Forces often incorrectly applied:
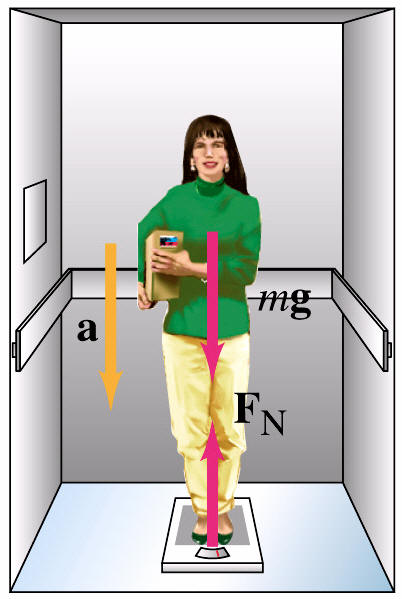
A 60-kg woman descends in an elevator in that briefly accelerates downward at
0.20g. If she stands on a scale, what is the reading on the scale (apparent
weight)?
Solution: Her apparent weight is the reading on the scale. According to
Newton's 3rd law, the force she exerts on the scale is also the force the scale
exerts on her (i.e., the normal force). As the elevator accelerates
downward, the application of Newton's laws shows that the reading on the scale
drops by 20% and she will indeed feel 20% lighter.
|
|
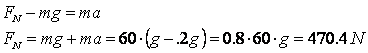 |
A new 230-kN Navy jet requires an airspeed of 85 m/s for liftoff. The engine
develops a maximum force of 101 kN, but that is insufficient for reaching
takeoff speed in the 90-m runway available on an aircraft carrier. What minimum
force (assumed constant) is needed from the catapult that is used to help launch
the jet? Assume that the catapult and the jet's engine each exert a constant
force over the 90 m distance used for takeoff.
Solution:
|
|
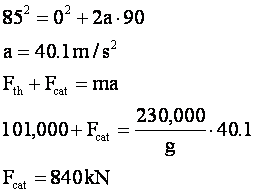 |
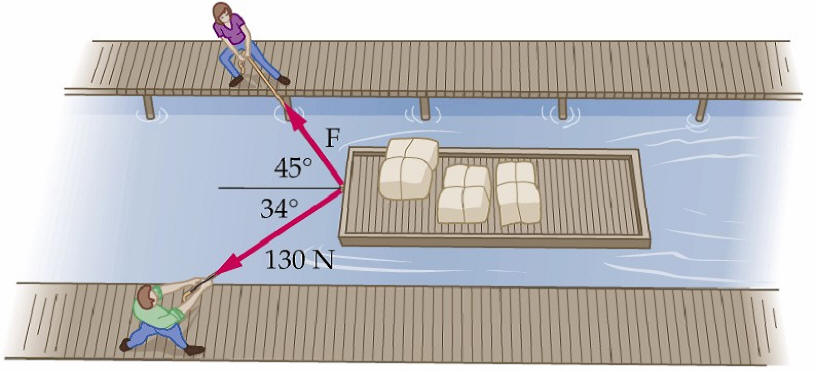
Sample problem: Two crewmen pull a boat through a lock, as shown. With
what force should the second crewman pull so that the net force of the two
crewmen is in the forward direction? If the boat moves at constant velocity,
what is the retarding force by the water?
Solution: Constant velocity implies zero acceleration, which in turn
implies the forces are balanced in the x- and y-directions.
 |
balancing the y-components gives: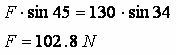 balancing the y-components gives: |
Sample problem: The record for the longest skid marks on a public road
was reportedly set in 1960 by a Jaguar on the M1 highway in England—the marks
were 290 m long! Assuming that μk = 0.60 and the car's acceleration
was constant during the braking, how fast was the car going when the wheels
became locked?
Solution:
Sample problem: Determine the speed of the Hubble space telescope
orbiting at an altitude of 598 km above the Earth's surface.
Solution: Note that the speed of any satellite of the Earth must be
between 8 km/s, which corresponds to LEO's (low Earth orbits), and 11.2 km/s,
which is the escape speed for the Earth.
![]()
Sample problem: The Space Shuttle is an example of a satellite in a
low-Earth orbit (LEO). It orbits at an altitude of about 100-200 km above the
Earth’s surface. What is the period of this orbit?
Solution: In this example, the distance to the center of the Earth (to be
used in the law of gravity) is almost the same as the radius of the Earth.
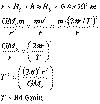
Sample problem: A geosynchronous satellite orbits the earth once per
day on a circular path that lies in the plane of the equator. What is the height
above the earth's surface at which all synchronous satellites must be placed in
orbit? Does this height depend on the mass?
Solution: Note that the altitude is the distance from the surface of the
Earth. However, the distance used in the law of gravity is always the distance
to the center of the Earth (or any other source of gravity).

Sample problem: A spring with a force constant of 115 N/m is used to
push a 0.27 kg block of wood against a wall. Find the minimum compression of the
spring needed to keep the block from falling, given that the coefficient of
static friction between the block and the wall is 0.43.
Solution: This problem involves a spring, which follow Hooke's law: F=-kx,
where k is the spring constant and x is the stretch or compression length for
the spring.
![]()
Return to class notes TOC.
Page last modified: