Solution:

Example: A 1000-kg Camaro collides into the rear end of a 3,000-kg
truck stopped at a red light in a school zone. The bumpers lock, the brakes are
locked, and the two cars skid forward 4.0 m before stopping. If the coefficient
of kinetic friction between tires and road is 0.40, what was the Camaro's speed
just before impact?
Solution:

Example: The 3.2-g is fired into the 850-g block of a ballistic
pendulum. The bullet sticks within the block, which swings back, rising 20 cm.
What was the speed of the bullet just before impact? What percentage of the
original kinetic energy was converted to heat?
Solution:
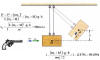
Example: A bullet is fired vertically into a 1.20 kg block of wood at
rest on a thin (assumed massless) horizontal sheet directly above it. If the
bullet has a mass of 29.0 g and a speed of 310 m/s, how high will the block rise
after the bullet becomes embedded in it?
Solution:

Example: At an intersection, a 1500-kg car traveling east at 25 m/s
collides with a 2500-kg van traveling north at 20 m/s. Find the velocity of the
wreckage immediately after the collision, assuming the two cars stick together.
Solution:
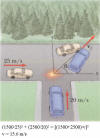
Example: Suppose Saturn is moving at its orbital speed (with respect
to the Sun) of 9.6 km/s. A spacecraft with mass 825 kg approaches Saturn, moving
initially in the opposite direction at 10.4 km/s. Estimate the final speed of
the spacecraft after it “slingshots” around and is far enough away to be nearly
free of Saturn's gravitational pull.
Solution:

Example: A 2.0-kg block slides along a frictionless tabletop at 8.0
m/s toward a second block (at rest) of mass 4.5 kg. A coil spring with a spring
constant k=850 N/m is attached to the second block in such a way that it will be
compressed when struck by the moving block. What is the maximum compression of
the spring and what is the velocity of the two blocks at this point?
Solution:
![]()
Example: A puck moving at 0.95 m/s in the x-direction makes a glancing
collision with a stationary puck. If the two pucks fly apart at 40° and 50°,
respectively, with respect to the x-axis, what is the speed of each puck after
collision?
Solution: This is a two-dimensional problem, so momentum has to be conserved
in both the x- and y-directions. Note that the two pucks fly apart at 90°, which
is true of all elastic collisions in 2D. Also, note that the kinetic energy
before collision is equal to the kinetic energy after collision, which must be
true in elastic collisions. This also implies that the relative speed of approach
is equal to the relative speed of recession. Why? (Think Pythagorean Theorem.)
![]()
Example: A 30-kg child in a 60-kg boat wants to propel the boat by
throwing out objects with a relative speed 10 m/s. If the objects all have a
mass of 5 kg and the friction between the boat and the water is 100 N (assumed
constant), at what rate does he need to expel the objects to maintain a speed of
5 m/s?
Solution: With each throw, the child receives an impulse equal to the
momentum imparted to the thrown object, as measured in the reference frame of
the child
(i.e.,
we use relative velocity).
![]()
Example: Suppose a fully fueled rocket has a mass of 21,000 kg, of
which 15,000 kg is fuel. The rate of exhaust is 190 kg/s with a relative exhaust
velocity of 2.8 km/s. If the rocket is launched vertically upward, what is the
velocity at burnout and how long does it take to reach this velocity?
Solution:

Example: A jet aircraft is traveling at 231 m/s in horizontal flight.
The engine takes in air at a rate of 80.0 kg/s and burns fuel at a rate of 2.20
kg/s. The exhaust gases are ejected at 570 m/s relative to the aircraft. Find
the thrust of the jet engine and the delivered power.
Solution: Perhaps the best way to visualize jet problems is to use the jet’s
reference frame. In this frame, air comes in with the velocity of the jet, the
jet then loses momentum to the air, combines the air with burnt fuel, and then
expels the mixture. Thus, thrust comes from the increase in momentum of the
air-fuel expulsion (momentum thrust). In addition, there may be some pressure
differences between the two ends of the jet. Here, we ignore pressure difference
between the two ends of the plane, which is a good approximation at subsonic
speeds.
![]()
Return to class notes TOC.
Page last modified: