Kinematics

Kinematics formulas

always true:

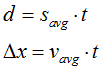
true only for constant acceleration:

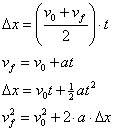
These formulas can be applied to two-dimensional kinematics simply by using the appropriate acceleration. For example, in projectile motion, only gravity is acting on the object in flight. Consequently, the horizontal acceleration is zero and the vertical acceleration has a value of g=9.8 m/s² pointing down (toward the ground).

Graphs

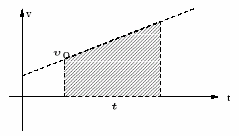
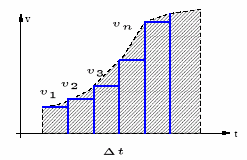
For a speed vs time graph, the area under the curve is equal to the distance.
For a velocity vs time graph, the area under the curve is equal to the displacement. Since velocity can be negative as well as positive, the displacement (and area) can also be negative and positive.
The slope of a velocity vs time graph is the acceleration.

Sample problem: A catapult accelerates the jet down the flight deck of an aircraft carrier. If the plane takes off with a velocity of 62 m/s after an acceleration of 31 m/s2, what is the length of the deck?
Solution:

Sample problem: A car speeding at 80 mph passes a stationary police car which immediately accelerates in an attempt to catch up to the speeder. What is the police car’s speed at the point of interception? If it takes the police car 10 seconds to catch up, what is its acceleration?
Solution:

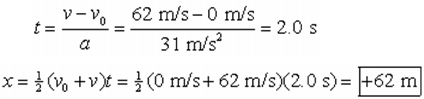
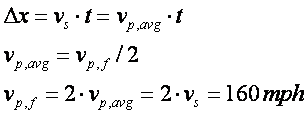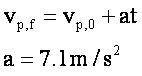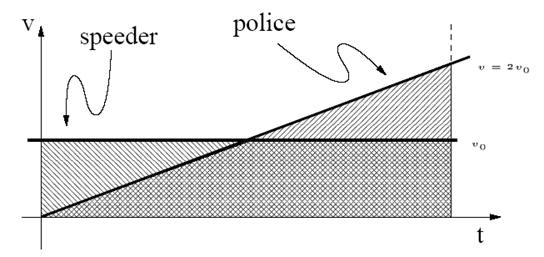Note that since the distance (and displacement) covered by the two cars during the same time interval is the same, the average speeds (velocities) must be the same. This implies that the maximum speed for the police car is twice the average speed.

Example: A motorcycle is moving at 39 m/s when the rider applies the brakes, giving the motorcycle a constant deceleration. If the speed decreases to 13 m/s after for 4.0 s of deceleration, how long does it take for the motorcycle to stop once breaking begins. What is the stopping distance?
Solution:

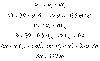
Example: A rocket rises vertically, from rest, with an acceleration of 3.0 m/s² until it runs out of fuel at an altitude of 1300 m. (a) What is the velocity of the rocket at this point? (b) How much higher will go? (c) What is total trip time (up and down)?
Solution: Because the acceleration changes over the course of the entire trip, the kinematics formulas must be applied at least twice, one for each region where acceleration does not change.

Return to class notes TOC.

Page last modified:

Kinematics formulas

Graphs

Sample problem: A catapult accelerates the jet down the flight deck of an aircraft carrier. If the plane takes off with a velocity of 62 m/s after an acceleration of 31 m/s2, what is the length of the deck? Solution:

Sample problem: A car speeding at 80 mph passes a stationary police car which immediately accelerates in an attempt to catch up to the speeder. What is the police car’s speed at the point of interception? If it takes the police car 10 seconds to catch up, what is its acceleration? Solution:

Sample problem: A catapult accelerates the jet down the flight deck of an aircraft carrier. If the plane takes off with a velocity of 62 m/s after an acceleration of 31 m/s2, what is the length of the deck?
Solution:

Sample problem: A car speeding at 80 mph passes a stationary police car which immediately accelerates in an attempt to catch up to the speeder. What is the police car’s speed at the point of interception? If it takes the police car 10 seconds to catch up, what is its acceleration?
Solution: