Heat conduction depends on the temperature gradient, cross section, path length, and the properties of materials. The expression is very similar to Ohm's Law for electric conduction. The analog of the voltage difference is the temperature difference, the analog of electric current is the heat flow rate, and the analog of electric resistance is thermal resistance (inverse of thermal conductance).
|
Substance
|
k (W/m·K)
|
|
|
|
|
Metals
|
|
|
Stainless steel
|
14
|
|
Lead
|
35
|
|
Aluminum
|
235
|
|
Copper
|
401
|
|
Silver
|
428
|
|
Gases
|
|
|
Air (dry)
|
0.026
|
|
Helium
|
0.15
|
|
Hydrogen
|
0.18
|
|
Building Materials
|
|
|
Polyurethane form
|
0.024
|
|
Rock wool
|
0.043
|
|
Fiberglass
|
0.048
|
|
White pine
|
0.11
|
|
Window glass
|
1.0
|
|
aConductivities
change somewhat with
temperature.
The given values are at room temperature.
|
|
Sample problem: Two rods, one lead and the other copper, are
connected in series between metal plates held at 2 °C and 106 °C. Both rods have
a length of 2 m and a diameter of 10 cm. Neglecting any heat flow through the
sides, what is the temperature at the lead-copper junction? What is the rate of
heat flow through the rods?
Solution: In this example, the two rods are in series and their thermal
"resistances" therefore add as electrical resistances do in series.

Sample problem: Two rods, one lead and the other copper, are connected
between metal plates held at 2 °C and 106 °C. If the rods have a diameter of 10
cm and are 2 m long, what is the rate of heat flow through the rods? Neglect any
heat flow through the sides.
Solution: In this example, the rods are in parallel and their thermal
"resistances" therefore add as electrical resistances do in parallel.



Sample problem: A 42-g ice cube at -10.0°C is placed in a Styrofoam
cup containing 350 g of water at 0°C. How much ice is in the water at
equilibrium?
Solution: In this problem, before setting up the equations, we need to
decide if the final system is at 0°C or lower. The wrong guess is not lethal. It
simply produces a temperature which falls outside the assumed range.

Sample problem: A 0.090-kg ice cube at 0 °C is dropped into a
Styrofoam cup holding 0.35 kg of water at 15 °C. Find the final temperature of
the system and the amount of ice (if any) remaining.
Solution: Once again, before setting up the equations, we need to decide
if the final system is at 0°C or lower. The wrong guess is not lethal. It simply
produces a temperature which falls outside the assumed range.

Sample problem: The filament of a light bulb has a temperature of
3000 °C and radiates 60 watts of power. The emissivity of the filament is 0.36.
Find the surface area of the filament.
Solution:
![]()
Sample problem: Suppose a person is unclothed and energy is being
lost via radiation from a body surface area of 1.40 m2, which has a temperature
of 34 °C and an emissivity of 0.7. Suppose also that metabolic processes are
producing energy at a rate of 115 W. What is the temperature of the coldest room
in which this person could stand and not experience a drop in body temperature?
Solution:
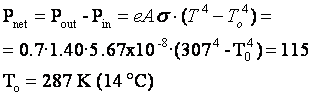
Sample problem: The supergiant star Betelgeuse has a surface temperature
of about 2900 K and emits a radiant power (in joules per second or watts) of
approximately P=4×1030 W, which is about 10,000 greater than that of
our Sun. Assuming that Betelgeuse is a perfect emitter (e = 1) and spherical,
find its radius.
Solution: The radius of Betelgeuse is twice the distance of the Earth
from the Sun, which is even greater than the distance of Mars to the Sun.
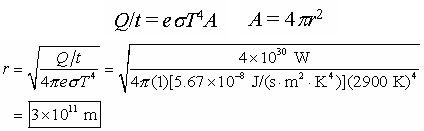
Return to class notes TOC.