A heat engine is a device that can take advantage of the natural flow of heat from hot to cold and convert some of the heat to useful work. The greater the conversion, the greater the efficiency of the heat engine.
Question: In Joule's famous paddle-wheel experiment (shown here), heat
is generated inside a water container as a result of a dropping weight. So
gravitational potential energy is converted first to the kinetic energy of the
paddle wheel and ultimately into heat. Can we reverse the process by heating up
the water and causing the weight to rise?
Answer: No. The random motion of water molecules hitting both sides of
each paddle wheel does not result in a net force on one side of each paddle. So
this heat engine would have an efficiency of zero.
Sample problem: Water near the surface of a tropical ocean has
a temperature of 298.2 K (25.0 °C), while water 700 m beneath the surface has a
temperature of 280.2 K (7.0 °C). It has been proposed that the warm water be
used as the hot reservoir and the cool water as the cold reservoir of a heat
engine. Find the maximum possible efficiency for such an engine.
Solution:
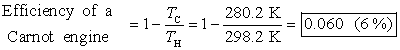
Sample problem: An engine removes 200 J from a hot reservoir at 373 K,
does some work, and exhausts 152 J to a cold reservoir at 273 K. How much energy
is “lost” per cycle due to irreversible processes?
Solution:

Sample problem: The steam engine which operates between 500°C and
280°C is run in reverse. How long would it take to freeze a tray of a dozen 36 g
compartments of liquid water at room temperature (20°C) into a dozen ice cubes
at the freezing point, assuming that it takes 480 W of input electric power to
run it? Assume ideal (Carnot) behavior.
Solution:
![]()
Sample problem: Suppose that water at room temperature of 29 °C
is put into an ideal refrigerator that maintains an inside temperature of -7 °C.
What is the cost of making 104 lb (46.8 kg) of ice if electricity costs $0.12
per kW·h?
Solution: The heat extracted from the water represents Qc.
This is the heat whch moves 'uphill' and dumped to the outside of the
refrigerator after being combined with the work W, which we pay for.
![]()
Question: Do you think a perpetual motion machine is possible? Study this youtube clip of a seemingly self-driven generator and try to figure out the energy source.
A gas in which the molecules occupy zero volume and do not interact with each other is known as an ideal gas. In practice, many gasses behave approximately like ideal gasses under ordinary conditions. The approximation improves at low pressure and high temperature. The advantage of discussing an ideal gas is that the equation of state is relative simple:
PV=nRT
where n is number of moles, R is the universal gas constant , and T is temperature in Kelvin. The value of R depends on the units used for pressure and volume. If atmospheres and liters are used then R=0.0821 L*atm/K/mole; if pascals are used, then R=8.314 J/K/mole (1 atm = 1.01x105 Pa).
The heat capacity of a substance refers to the ability of a substance to resist a change in temperature when heat is added to the substances.
Water has one of the largest heat capacities of any substance and for that reason resists has a very strong moderating effect on our climate. Heat capacity can be measured by adding a known quantity of heat to a substance and then measuring the temperature change. The ratio of the two quantities gives us the heat capacity:
![]()
In general, heat capacity depends on the conditions under which heat is transferred. The two most common situations involve either a constant pressure or a constant volume. An experiment performed in an open beaker is considered a constant-pressure process, the pressure being one atmosphere. An experiment performed in a closed solid container is considered a constant-volume process. The heat capacity at constant pressure Cp is generally greater than the heat capacity at constant volume Cv because some energy is "absorbed" in expansion work, which tends to reduce the temperature change. For solids, the difference is not very large since solids do not expand very much and the distinction is thus often not made. For gasses, the difference is relatively large. For ideal gasses, Cp - Cv = R (per mole).
Every kind of molecule has a certain number f of degrees of freedom, which are independent ways in which the molecule can store energy. Each such degree of freedom has associated with it—on average—an energy of kT/2 per molecule (or RT/2 per mole). For a monatomic molecule, the number of degrees of freedom is 3, corresponding to motion (translation) along the x-, y-, and z-axes. Consequently, the average kinetic energy per mole for a monatomic gas is 3*RT/2. Diatomic molecules can store energy in rotation as well as in translation. Since diatomic molecules can rotate along 2 independent axis (the third one corresponds to zero moment of inertia), they have 2 additional degrees of freedom. Polyatomic molecules can store energy by rotating about 3 independent rotational axes and thus have 3+3=6 degrees of freedom.
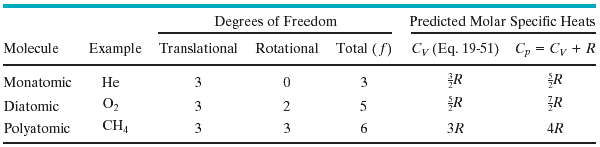
Gas molecules can also have vibrational degrees of freedom, but these are generally "frozen out" (not active) at ordinary temperatures. In general, the energy of a gas molecule is given by:
![]()
Sample problem: One mole of an ideal monatomic gas is taken
through the cycle shown. Assume that p = 2p0, V = 2V0,
p0 = 1.08x105 Pa, and V0 = 0.0244 m3.
What is the efficiency of this cycle? What is the ideal efficiency of a
heat engine operating between the highest and the lowest temperature?
Solution: A good way to start this problem is to label every vertex with
pressure, volume, and temperature. The path abc is the heat-intake (Qh)
portion of the cycle. In path ab, the pressure doubles at constant
volume. The ideal gas law (PV=nRT) implies that the temperature also
doubles. Since work is zero along path ab, the internal energy change is
equal to the heat input (Q1). Similarly, along path bc, the
volume doubles at constant pressure and the ideal gas law (PV=nRT)
implies that the temperature also doubles. Since
Wbc (expansion work) is positive
and ΔUbc=Qbc-Wbc >0, Qbc
must be positive and greater than Wbc. Using similar
reasoning, the temperature drops by a factor of 2 along path cd and then
drops by a factor of 2 again along path da.
![]()
Sample problem: Suppose 9 moles of a monatomic ideal gas follows
the three-part cycle, the first part of which involves an isothermal
expansion from point A, where V = 7.5x10-5 m3 and
P=6x105 Pa, to point B, where the pressure is lower by a
factor of 6. What is the efficiency of the cycle? What is the ideal
efficiency of an engine operating between the highest and lowest
temperature of this cycle?
Solution: The important idea in this problem is that pressure and volume
are inversely related along an isotherm. If pressure goes up by a
certain factor, the volume drops by the same factor.

Sample problem: Two moles of a monatomic ideal gas are taken
through the reversible cycle shown. Process ab is an isometric increase
in pressure. Process bc is an adiabatic
expansion, with Pb = 11.9 atm, Vb = 10 L, and Vb
= 8*Va. Process cb is an isobaric compression. Find
the efficiency of the cycle and the maximum efficiency for the
temperature extremes of the cycle.
Solution: Note that for a complete cycle, ΔU=0,
which implies that W=Q. Calculating heat in this example is pretty
straightforward because the two heat generating legs involve either a
constant pressure or a constant volume, which means Qab=ncpΔT
or Qca=ncvΔT, respectively. The adiabatic process
bc generates no heat.

Sample problem: Suppose 5 moles of a monatomic ideal gas are
taken through the following three-part cycle: isochoric (same volume)
pressure increase by a factor of 3, expansion along a straight
line on a P-V diagram, isobaric compression by a factor of 4. What is
the efficiency of the cycle? What is the ideal efficiency of an engine
operating between the highest and lowest temperature of this cycle?
Solution: Along path CA, dQ=dU, so the increase in temperature implies
heat is flowing into the gas. Along path AB, energy is lost as work, yet
total energy increases. This implies that heat is flowing into the gas.
