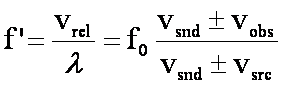
The Doppler effect, named after Christian Doppler, is the change in frequency and wavelength of a wave as perceived by an observer moving relative to the source of the waves. For waves that propagate in a wave medium, such as sound waves, the velocity of the observer and of the source are calculated relative to the medium in which the waves are transmitted. The total Doppler effect may therefore result from either motion of the source or motion of the observer.
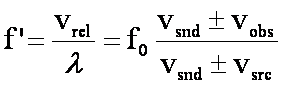
where vrel is the relative speed between the pulse and the observer and vsnd is the speed of sound. Wind has essentially the same effect as an increase or decrease in sound velocity. If the crests are moving with the wind (in the same direction as the wind), then sound velocity is effectively increased. This has two competing effects on the perceived frequency. On the one hand, frequency should go down because the wavelength increases. When neither the source nor the observer is moving, the two effects completely cancel and the perceived frequency is the source frequency. On the other hand, the frequency should go up because the observer is running into the crests more frequently. The reverse logic holds when the crests are moving against the wind.
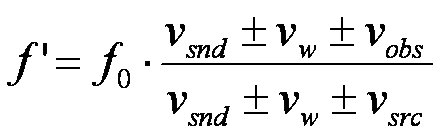
Sample problem: A train sounds its whistle as it approaches a
tunnel in a cliff. The whistle produces a tone of 650 Hz. If it travels at a
speed of 21.2 m/s, what is the frequency heard in the tunnel and in the
reflected sound?
Solution:
Sample problem: A high-speed train is traveling at a speed of 44.7 m/s
(100 mi/h) when the engineer sounds the 415-Hz warning horn. The speed of sound
is 343 m/s. What are the frequency and wavelength of the sound, as perceived by
a person standing at a crossing, when the train is (a) approaching and (b)
leaving the crossing?
Solution: When the train approaches, the person at the crossing hears a
sound whose frequency is greater than 415 Hz because the wavelength has
effectively decreased. As the train moves away, the person hears a frequency
that is less than 415 Hz because the wavelength has effectively increased.
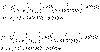
Sample problem: A girl is sitting near the open window of a train that is
moving at a velocity of 23 m/s to the east. The girl's baby brother stands near
the tracks and watches the train move away. The locomotive whistle emits sound
at a frequency of 580 Hz. Assume that the speed of sound in still air is 343
m/s. (a) What frequencies do the girl and brother hear? (b) How would your
answers change if a wind now blows from the east at 9.2 m/s.
Solution:
![]()
When the source of a wave moves faster than wave itself, an interference pattern forms in which constructive interference occurs along a conical surface known as a shockwave. When this occurs with sound, the shockwave gives rise to a loud sound known as a sonic boom. For a commercial supersonic transport plane (SST), the sonic boom can be as loud as 136 decibels, or 120 Pa (in units of pressure). This applet demonstrates the cone effect and this applet applies the effect to a moving plane.
Sample problem: A supersonic jet traveling at Mach 1.8 at an altitude of
10 km passes directly over an observer on the ground. How far ahead will the
plane be when the observer hears the sonic boom?
Solution:
![]()
Sample problem: A supersonic aircraft is flying parallel to the ground.
When the aircraft is directly overhead, an observer sees a rocket fired from the
aircraft. 10 s later the observer hears the sonic boom, followed 2.80 s later by
the sound of the rocket engine. What is the Mach number of the aircraft?
Solution:
![]()
Return to class notes TOC.