Solution:

Acceleration is defined as the rate of change of velocity. Since velocity is a vector, it can change in magnitude as well as in direction. When the magnitude of the velocity (i.e., speed) remains the same, only the change in direction contributes to the acceleration. This contribution is always centripetal (i.e., points toward the center) and has a magnitude equal to v2/r. A large number of interesting problems involve a constant speed and a constant radius. These problem fall under the heading of uniform circular motion. If the speed is also changing, the acceleration then consists of two perpendicular components, one centripetal and one tangential.
Sample problem: The Gagarin Cosmonaut Training Center is used to train
Russian cosmonauts for space missions. If the device can rotate at 25 rpm and
has a radius of rotation of about 20 m, what acceleration does the trainee
experience?
Solution:

Sample problem: If the tubes of a centrifuge spin at a rate of 170 rps
and the bottom of the tubes is 8.5 cm from the axis of rotation, what force is
exerted on the bottom of the test tube by a 12-g bolus?
Solution:
![]()
Sample problem: The design of a new road includes a straight stretch
that is horizontal and a flat but that suddenly dips down a steep hill at 22°.
The transition should be rounded with what minimum radius so that cars traveling
90 km/h will not leave the road?
Solution: The important consideration here is that when the car is just
about to leave the road, the normal force goes to zero. Note also that the mass
of the car is irrelevant.
![]()
Sample problem: A daredevil stunt involves riding a motorcycle around
the vertical inside wall of a cylindrical structure. If the cylinder has a
radius of 15 m and the coefficient of static friction between the motorcycle
tires and the wall is 1.1, what is the minimum speed that will keep the
motorcycle and the rider from sliding down the wall?
Solution: In this problem, the centripetal force is the normal force.
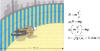
Sample problem: In 1901, Allo "Dare Devil" Diavolo rode a bicycle upside
down in a circus performance, seemingly defying the laws of physics. But did
he? Assuming that Allo's pedaling just compensates for friction, what is the
minimum speed of approach that Allo must have as he enters the loop of radius
2.7 m if he is to maintain contact with the loop?
Solution: In this problem, the centripetal force is the normal force.
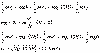
Sample problem: A hockey puck of mass m = 200 g on a frictionless
table is attached to a hanging mass M = 5 kg by a cord through a hole in the
table. Find the speed with which the puck must move (in a circle of radius r =
0.15 m) in order for M to stay at rest.
Solution:

When a car travels without skidding around an unbanked (perfectly horizontal)
curve, the static frictional force between the tires and the road provides the
necessary centripetal force. The reliance on friction can be eliminated
completely for a given speed, however, if the curve is banked at an angle
relative to the horizontal, much in the same way that a plane is banked while
making a turn.
Sample
problem: The turns in the Daytona International Speedway in Daytona, Florida
have a maximum radius (at the top) of r = 316 m and are banked steeply, with θ =
31°. Suppose these maximum-radius turns were frictionless. What would be the
maximum speed for these turns?
Solution: In the absence of friction, the horizontal component of the
normal force provides the necessary centripetal force. A car moving too fast for
a given radius and banking angle would skid radially out. A car moving too
slowly would skid inward.

Sample
problem: An airplane is flying in a horizontal circle at a speed of 480 km/h
(133 m/s). If its wings are tilted 40° to the horizontal, what is the radius of
the circle in which the plane is flying? Assume that the required force is
provided entirely by an “aerodynamic lift” that is perpendicular to the wing
surface.
Solution: Note the similarity of this problem to the car on a banked
road.
![]()
Return to class notes TOC.
Page last modified: