Capacitance
Sample problem: In lightning storms, the potential difference between the
Earth and the bottom of the thunderclouds can be as high as 25,000,000 V. The
bottoms of the thunderclouds are typically 1500 m above the Earth, and can have
an area of 140 km2. For the purpose of this problem, model the Earth-cloud
system as a huge capacitor. If this capacitor takes about half an hour to
discharge, how much (average) power can be delivered to Earth during this time?
Solution:
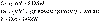
Sample problem: A storage capacitor on a random access memory (RAM) chip
has a capacitance of 55 fF. If the capacitor is charged to 5.3 V, how many
excess electrons are on its negative plate?
Solution:
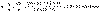
Sample problem: A commercial capacitor is constructed as by rolling two
strips of aluminum separated by two strips of paraffin-coated paper. Each strip
of foil and paper is 7.50 cm wide. The foil is 0.00400 mm thick, and the paper
is 0.025 mm thick and has a dielectric constant of 3.7. What length should the
strips be if a capacitance of 9.8x10-8 F is desired? (Model the
capacitor as parallel plates.)
Solution:
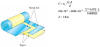
Sample problem: What is the maximum charge that an air-filled
parallel-plate capacitor with A=1 m2 and d=1 mm can hold? What is the
maximum charge for the same capacitor filled with teflon?
Solution: In this example, the charge increases for two reasons: an
increase in the maximum voltage (factor of 20) due a greater dielectric strength
and an increase in the capacitance (factor of 2.1) due to a higher dielectric
constant, for a combined factor of 42.
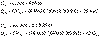
Sample problem: In this parallel-plate capacitor, a potential difference
of V0 = 82 V is applied across the plates. A dielectric slab of
thickness b = 0.78 cm and dielectric constant 2.55 is now introduced while the
battery remains connected. Calculate the charge on the plates and the
capacitance if the plate area A = 100 cm2 and plate separation d =
1.15 cm.
Solution:

Sample problem: A wafer of titanium dioxide (dielectric constant = 173)
has an area of 1.15 cm2 and a thickness of 0.13 mm. Aluminum is
evaporated on the parallel faces to form a parallel-plate capacitor. What is the
capacitance and electric field. When the capacitor is charged with a 12.0 V
battery, what is the magnitude of charge delivered to each plate? What are the
free and induced surface charge densities? What is capacitance and magnitude of
the electric field?
Solution:
Return to class notes TOC.
Page last modified: