Solution:

This applet demonstrates the exponential nature of charging of a capacitor.
Sample problem: If the capacitor is initially uncharged, what is the
charge after a long time? How long will it take the capacitor to reach 80% of
full charge?
Solution:

Sample problem: Assuming the capacitor is initially discharged, what
current is drawn from the battery right after the switch is closed? After a long
time?
Solution: Initially, the discharged capacitor acts as a short circuit.
After a long time, the capacitor becomes fully charged and acts as an open
switch.
![]()
Sample problem: What is the current through the switch right after the
switch is closed? What is the current a long time after the switch is closed?
What is the voltage and charge on the fully charged capacitor? After the switch
is opened, how long does it take for the capacitor to discharge to 5% of its
full charge?
Solution:

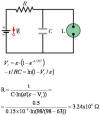
Sample problem: Suppose there is a current through the lamp only when
the potential difference across it reaches the breakdown voltage VL.
In this event, the capacitor discharges completely through the lamp and the lamp
flashes briefly. Suppose that two flashes per second are needed. For a lamp with
breakdown voltage VL = 63 V, wired to a 98 V ideal battery and a 0.15
μF capacitor, what should be the resistance R?
Solution: Two flashes per second implies that the capacitor discharges
after 0.5 seconds of charging, then charges for 0.5 seconds, then discharges
again, and so on. The charging follows the usual exponential time dependence, as
if the lamp were not there. The only difference is that the capacitor never
reaches its maximum voltage of 98 V.
Sample problem: Two resistors are connected in series (R and 100 Ω)
with an inductor (L=75 mH) and an emf=36 V. After the switch is closed for a
long time, the energy stored in the inductor is 3 mJ. What is the value of R?
Solution:
![]()
Sample problem: When the switch is closed, the current in the circuit
is observed to increase from 0 to 0.2 A in 0.15 seconds. What is the maximum
current in the circuit? How long after the switch is closed does the current
have 0.4 A?
Solution:
![]()
Return to class notes TOC.
Page last modified: