Stellar magnitude

Apparent and Absolute Magnitude

Historically, stars were classified by position in the sky and apparent brightness, as seen from Earth with the unaided eye.
Apparent brightness was defined using the magnitude scale.
- The faintest object that can be seen with the naked eye is assigned a magnitude of 6.
- The brighter an object, the smaller its magnitude. Although this convention may seem counterintuitive, it leaves room on the high-magnitude side for the discovery of increasingly faint objects.
- The scale is logarithmic so that differences in magnitude correspond to ratios of brightness. A difference of 5 magnitudes corresponds to a brightness ratio of 100. A magnitude 1 star is thus 100 times brighter (as measured by an instrument) than a magnitude 6 star. A magnitude difference of 2.5 corresponds to a factor of 10 in brightness.
A term related to, and often confused with, brightness is luminosity. Luminosity is defined as the rate at which a star (or other bright object) radiates light energy. Luminosity is proportional to the surface area of a star and to the fourth power of its surface temperature (T⁴). The apparent brightness of any star in the sky is defined as the amount of light reaching us per unit area. (A more technical term for apparent brightness is flux.) Apparent brightness falls off with distance according to the well-known inverse-square law: dilution factor=1/d². For example, a light bulb appears dimmer at 20 feet than at 10 feet by a factor of 2²=4, dimmer at 30 feet than at 10 feet by a factor of 3²=9 , dimmer at 40 feet by a factor of 4²=16, and so on.
The magnitude scale was originated by the Greek astronomer Hipparchus around 129 B.C., when he produced the first well-known star catalog.
- Hipparchus ranked his stars in a simple way. He called the brightest ones "of the first magnitude," simply meaning "the biggest." Stars not so bright he called "of the second magnitude," or second biggest. The faintest stars he could see he called "of the sixth magnitude." Thus, when the ancient Greeks looked at the sky, they saw only a few thousand stars, all brighter than magnitude 6.
- In 1610, when Galileo pointed his first telescope at the stars, he found tens of thousands more, fainter than magnitude 6, but brighter than about magnitude 9.
- As telescopes got bigger and better, astronomers kept adding more magnitudes to the bottom of the scale. Today, a pair of 50-millimeter binoculars will show stars of about 9th magnitude, a 6-inch amateur telescope will reach to 13th magnitude, and the Hubble Space Telescope has seen objects as faint as 31st magnitude. Furthermore, with quantitative measurement of brightness and recalibration, some objects in the sky were relabeled with negative magnitudes.
- By the middle of the 19th century, astronomers realized there was a pressing need to define the entire magnitude scale more precisely than by eyeball judgment. They had already determined that a 1st-magnitude star shines with about 100 times the light of a 6th-magnitude star. Accordingly, in 1856 the Oxford astronomer Norman R. Pogson proposed that a difference of five magnitudes be exactly defined as a brightness ratio of 100 to 1. This convenient rule was quickly adopted. One magnitude thus corresponds to a brightness difference of exactly the fifth root of 100, or very close to 2.512 — a value known as the Pogson ratio.
- A star that is one magnitude number lower than another star is about two-and-a-half times brighter. A magnitude 3 star is 2.5 times brighter than a magnitude 4 star. A magnitude 4 star is 2.5 times brighter than a magnitude 5 star.
- The logarithmic nature of the magnitude scale is analogous to the Richter Scale for earthquakes, where a 5.0 is ten times stronger than a 4.0, which is ten times stronger than a 3.0. On the Richter scale, a difference of "one" on the scale means a factor of ten in earthquake strength.
The magnitude of an object as measured on Earth is known as apparent magnitude. Because objects in the sky are all at different distances from us, apparent magnitude (from the perspective of an observer on Earth) is not a true measure of an object's intrinsic brightness (luminosity). Is our Sun bright because it generates a lot of power or because it's very close to us?
To eliminate the "diluting" effects of distance, astronomers have come up with a better measure of intrinsic brightness called absolute magnitude, which is defined as the apparent brightness an object would have if it were located exactly 10 parsecs (about 32.6 light years) away from Earth. By this measure, our Sun, with an absolute magnitude of 4.83, is not an especially bright star.
To the ancients, distance was not considered a critical factor because stars were believed to be fixed on the Celestial Sphere centered on the Earth, and thus all at the same (unknown) distance from us.
Click here to see what different-magnitude stars in Orion might look like under different lighting conditions.

Example: 2 stars (A and B) with the same absolute magnitude have apparent magnitudes m=1 (A) and m=6 (B). How much more distant is B than A?
Solution: A difference of 5 in apparent magnitude corresponds to a factor of 10x10=100 in brightness. Since brightness drops off as the square of the distance, the dimmer star (B) is 10 times farther away.

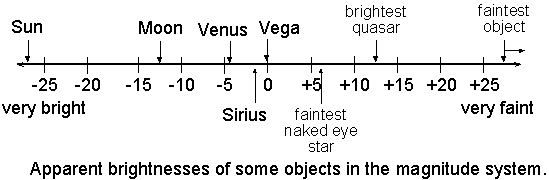
magnitude system

Object	app mag	distance (ly)	abs mag
Sun	-26.7	1/60,000	4.8
Moon (full)	-12.5	---	---
Sirius (α Sco)	-1.5	8.6	1.4
Venus (brightest)	-4.4	---	---
Mars (brightest)	-2.9	---	---
Jupiter (brightest)	-2.8	---	---
Vega (α Lyr)	0	25	0.58
Betelgeuse	0.45	430	-5.1
Rigel	0.12	800	-6.7
Saturn (brightest)	0.6	---	---
Polaris	2.0	430	-3.6
naked-eye limit	6
Ceres	6.7		---
binocular limit	10
Pluto/20 cm telescope	14		---
Hubble limit	30
***Note that planets and the Moon can only reflect light, so assigning absolute magnitude in these cases is meaningless.

Conversion of Magnitude to Brightness Ratios
A magnitude difference of:	Equals a brightness ratio of:
0.0	1.0
0.2	1.2
1.0	2.5
1.5	4.0
2.0	6.3
2.5	10.0
4.0	40.0
5.0	100.0
7.5	1000.0
10.0	10,000.0

Naked-eye sky objects

There are ten natural solar system objects you can see without optical aid.

The Sun. No surprise here. The Sun shines at magnitude -26.7. Technically, the Sun can't even be looked at without optical aid when it is at its brightest. Sunrise and sunset are the best times to view our closest star.
The Moon. The moon varies in brightness depending on what phase it is in. At its full phase when it is the brightest, it tops out at magnitude -12.6, and in a crescent phase it is about a -6.
Venus. As with all the other solar system objects, Venus varies in brightness depending on a number of factors, including how close it is to Earth and what phase it is in. Venus can shine as brightly as -4.4 and is frequently referred to as the Evening Star or the Morning Star.
Mars. Mars is the second closest planet to Earth after Venus, but it does not often reach its maximum magnitude of -2.9. Its reddish-orange hue helps to distinguish it from other planets.
Jupiter. This gas giant is often brighter than Mars and at its maximum shines almost as bright, at magnitude -2.8.
Mercury. Surprise! The rarely seen Mercury shines more brightly than Saturn at its best. Mercury can reach -1.9 magnitude but because of its position near the Sun, it does not get to be seen high in the night sky. Its brightness is often offset by the fact that you are viewing the planet near sunrise and sunset.
Saturn. Saturn, which is stunning in a telescope sporting wide rings, is also a fairly easy catch without optical aid. At magnitude 0.7 it outshines most stars.
Ganymede. Ganymede is the largest moon of Jupiter. Keen eyes can spot it circling Jupiter when the satellite is at its brightest, approximately 4.6 magnitude.
Vesta. This asteroid, which was the fourth asteroid to be discovered, can reach magnitude 5.4 at its closest approach to Earth. Because it does not have a brighter sky marker, as Ganymede has with Jupiter, it is best to watch for it a couple nights in a row to see which dim "star" in the area appears to slowly move.
Uranus. The seventh planet from the Sun appears at magnitude 5.5 at its best. Uranus is best picked up with the naked eye after first pinning down its location with binoculars or a telescope. It has a disk instead of a pinpoint image through an optical device and may even appear faintly bluish green.

Ceres is a bright asteroid but at magnitude 6.7, it would be a real trick to pick out with the eyes alone. Neptune at magnitude 7.7 and Pluto at 13 require optical aid. (Pluto, in particular, requires a large telescope.) There are also transient solar system objects that occasionally appear bright enough to be seen without optical aid, such as meteors or comets.

Return to class notes TOC.

Page last modified: