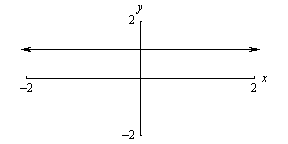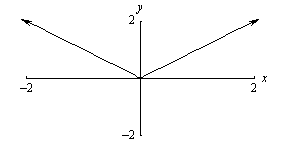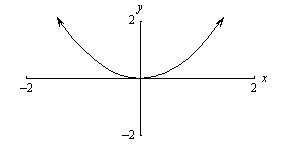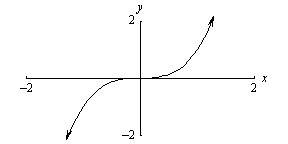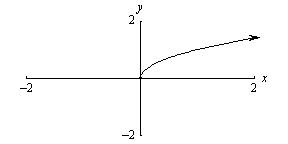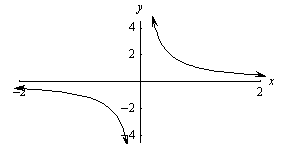These are also called the "elementary functions." A partial list is given
in section 2.5.
| Name and Definition |
Graph |
Domain and Range |
Important Points and Comments |
| Constant c(x) = 1 |
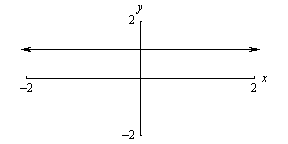 |
D: { x | x Î
Ñ }
R: { y | y = 1 } |
All horizontal lines are classified as constants. Even
function. |
| Linear or Identity Function f(x) = x |
 |
D: { x | x Î
Ñ }
R: { y | y Î
Ñ } |
Goes thru the origin (0,0) Odd function |
| Absolute Value g(x) = | x | |
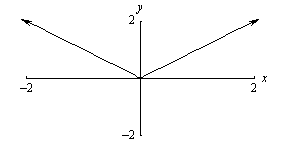 |
D: { x | x Î
Ñ }
R: { y | y ³ 0
} |
Goes thru the origin (0,0) Even function
|
| Quadratic h(x) = x^2 |
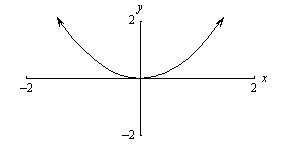 |
D: { x | x Î
Ñ }
R: { y | y ³ 0
} |
Goes thru the origin (0,0), (1,1), and (-1,1) Even
function
|
| Cubic m(x) = x^3 |
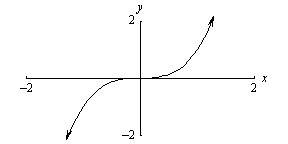 |
D: { x | x Î
Ñ }
R: { y | y Î
Ñ } |
Goes thru the origin (0,0), (1,1), and (-1,-1) Odd
function
|
| Square Root n(x) = x^(1/2) |
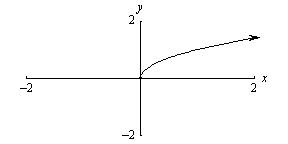 |
D: { x | x ³ 0
} R: { y | y
³ 0
} |
Goes thru the origin (0,0) and (1,1) No symmetry |
| Cube Root p(x) = x^(1/3) |
 |
D: { x | x Î
Ñ }
R: { y | y Î
Ñ } |
Goes thru the origin (0,0), (1,1), and (-1,-1) Odd
function
|
| Reciprocal r(x) = 1/x |
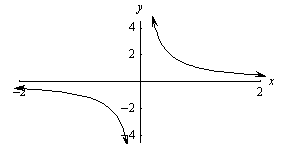 |
D: { x | x ³ 0
or x
£ 0
} R: { y | y
³ 0
or y
£ 0
}
|
Goes thru the origin (0,0), (1,1), and (-1,-1) Odd
function
Horizontal asymptote at y = 0
Vertical asymptote at x = 0
|
| Sine Function s(x) = sin(x) |
 |
D: { x | x Î
Ñ }
R: { y | -1
£ y
£ 1 } |
Goes thru the origin (0,0) Odd function
Sine is 2*pi periodic |
| Exponential t(x) = 2^x |
 |
D: { x | x Î
Ñ }
R: { y | y > 0
} |
Goes thru the origin (0,0), (1,2), and (-1,1/2). No
symmetry
Horizontal asymptote at y = 0
The general exponential b^x, b>0 and not b = 1 goes thru (1,b) and
(-1,1/b).
The case where 0 < b < 1 gives a graph similar to 2^x except reflected
about the y axis. |